This page examines the properties of two-dimensional or ‘plane’ polygons.  A polygon is any shape made up of straight lines that can be drawn on a flat surface, like a piece of paper. Such shapes include squares, rectangles, triangles and pentagons but not circles or any other shape that includes a curve.

Understanding shapes is important in mathematics. You will certainly be required to learn about shapes at school but understanding the properties of shapes has many practical applications in professional and real-life situations too.

Many professionals need to understand the properties of shapes, including engineers, architects, artists, real-estate agents, farmers and construction workers.

You may well need to understand shapes when doing home improvements and DIY, when gardening and even when planning a party.

---

Number of Sides

Polygons are usually defined by the number of sides that they have.

Three-Sided Polygons: Triangles

A three-sided polygon is a triangle. There are several different types of triangle (see diagram), including:

• Equilateral – all the sides are equal lengths, and all the internal angles are 60°.
• Isosceles – has two equal sides, with the third one a different length. Two of the internal angles are equal.
• Scalene – all three sides, and all three internal angles, are different.

Triangles can also be described in terms of their internal angles (see our page on Angles for more about naming angles). The internal angles of a triangle always add up to 180°.

A triangle with only acute internal angles is called an acute (or acute-angled) triangle. One with one obtuse angle and two acute angles is called obtuse (obtuse-angled), and one with a right angle is known as right-angled.

Each of these will also be either equilateral, isosceles or scalene.

---

Four-Sided Polygons - Quadrilaterals

Four-sided polygons are usually referred to as quadrilaterals, quadrangles or sometimes tetragons. In geometry the term quadrilateral is commonly used.

The term quadrangle is often used to describe a rectangular enclosed outdoor space, for example ‘the freshers assembled in the college quadrangle’. The term tetragon is consistent with polygon, pentagon etc. You may come across it occasionally, but it is not commonly used in practice.

The family of quadrilaterals includes the square, rectangle, rhombus and other parallelograms, trapezium/trapezoid and kite.

The internal angles of all quadrilaterals add up to 360°.

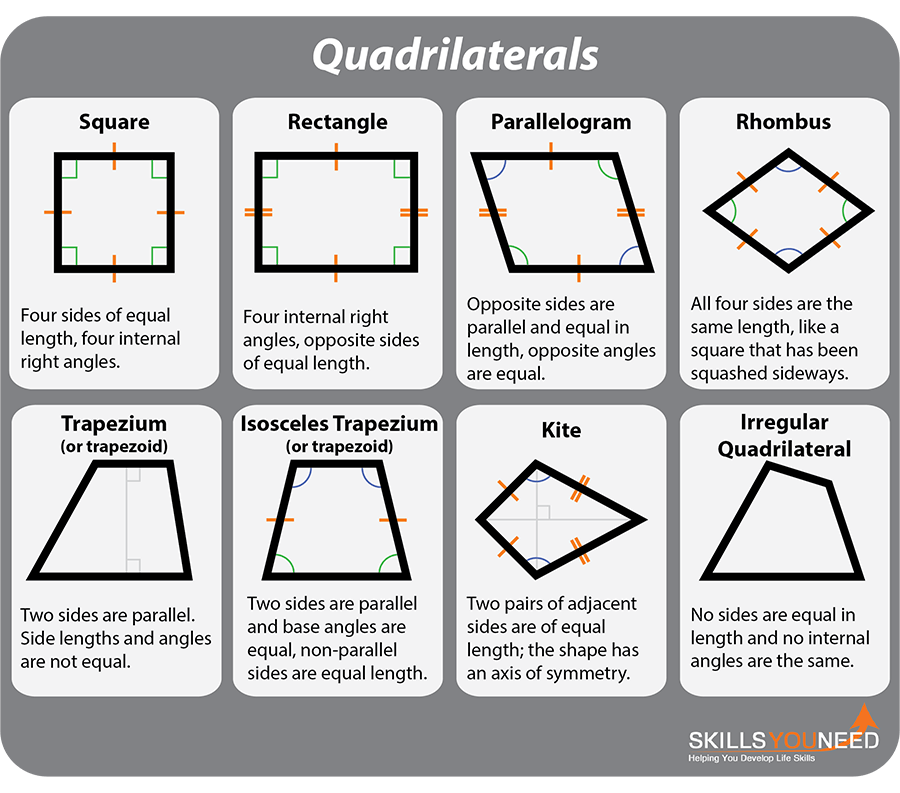
• Square: Four sides of equal length, four internal right angles.

• Rectangle: Four internal right angles, opposite sides of equal length.

• Parallelogram: Opposite sides are parallel, opposite sides are equal in length, opposite angles are equal.

• Rhombus: A special type of parallelogram in which all four sides are the same length, like a square that has been squashed sideways.

• Trapezium (or trapezoid): Two sides are parallel, but the other two sides are not. Side lengths and angles are not equal.

• Isosceles Trapezium (or trapezoid): Two sides are parallel and base angles are equal, meaning that non-parallel sides are also equal in length.

• Kite: Two pairs of adjacent sides are of equal length; the shape has an axis of symmetry.

• Irregular Quadrilateral: a four-sided shape where no sides are equal in length and no internal angles are the same. All internal angles still add up to 360°, as with all other regular quadrilaterals.

---

---

More than Four Sides

A five-sided shape is called a pentagon.

A six-sided shape is a hexagon, a seven-sided shape a heptagon, while an octagon has eight sides…

There are names for many different types of polygons, and usually the number of sides is more important than the name of the shape.

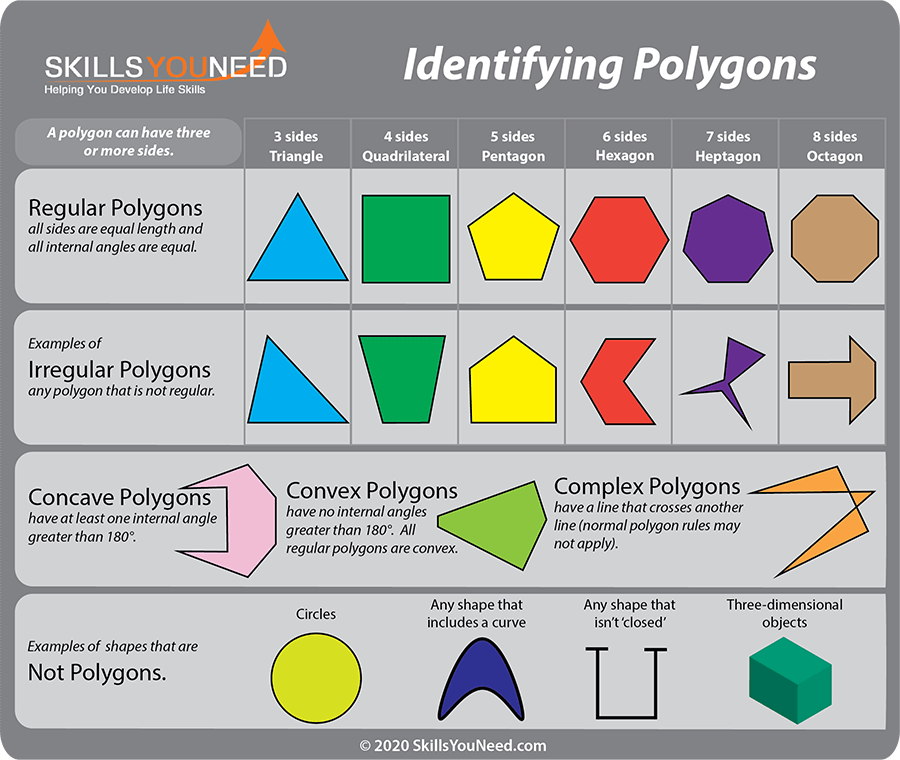
There are two main types of polygon - regular and irregular.

A regular polygon has equal length sides with equal angles between each side. Any other polygon is an irregular polygon, which by definition has unequal length sides and unequal angles between sides.

Circles and shapes that include curves are not polygons - a polygon, by definition, is made up of straight lines. See our pages on circles and curved shapes for more.

---

Angles Between Sides

The angles between the sides of shapes are important when defining and working with polygons. See our page on Angles for more about how to measure angles.

---

The Length of the Sides

As well as the number of sides and the angles between sides, the length of each side of shapes is also important.

The length of the sides of a plane shape enables you to calculate the shape’s perimeter (the distance around the outside of the shape) and area (the amount of space inside the shape).

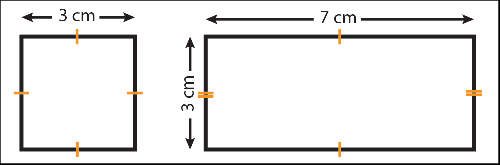
If your shape is a regular polygon (such as a square in the example above) then it is only necessary to measure one side as, by definition, the other sides of a regular polygon are the same length. It is common to use tick marks to show that all sides are an equal length.

In the example of the rectangle we needed to measure two sides - the two unmeasured sides are equal to the two measured sides.

It is common for some dimensions not to be shown for more complex shapes. In such cases missing dimensions can be calculated.

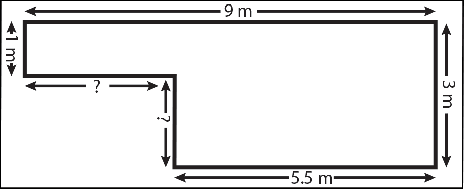
In the example above, two lengths are missing.

The missing horizontal length can be calculated. Take the shorter horizontal known length from the longer horizontal known length.

9m - 5.5m = 3.5m.

The same principle can be used to work out the missing vertical length. That is:

3m - 1m = 2m.

---

Bringing All the Information Together: Calculating the Area of Polygons

The simplest and most basic polygon for the purposes of calculating area is the quadrilateral. To obtain the area, you simply multiple length by vertical height.

For parallelograms, note that vertical height is NOT the length of the sloping side, but the vertical distance between the two horizontal lines.

This is because a parallelogram is essentially a rectangle with a triangle cut off one end and pasted onto the other:

You can see that if you remove the left-hand blue triangle, and stick it onto the other end, the rectangle becomes a parallelogram.

The area is length (the top horizontal line) multiplied by height, the vertical distance between the two horizontal lines.

To work out the area of a triangle, you multiple length by vertical height (that is, the vertical height from the bottom line to the top point), and halve it. This is essentially because a triangle is half a rectangle.

To calculate the area of any regular polygon, the easiest way is to divide it into triangles, and use the formula for the area of a triangle.

So, for a hexagon, for example:

You can see from the diagram that there are six triangles.

The area is:

Height (red line) × length of side (blue line) × 0.5 × 6 (because there are six triangles).

You can also work out the area of any regular polygon using trigonometry, but that’s rather more complicated.

See our page Calculating Area for more, including examples.

You can also work out the area of any regular polygon using trigonometry, but that’s rather more complicated. See our Introduction to Trigonometry page for more information.

---